線積分は3年前くらいに習ったと思うのですが、以来まったく使ってこなかったのですっかり忘れてしまいました。思い出せるようにメモしていきます。

1. 積分

「積分と同じやろ」と思って計算していたら、それは面積を計算しているのと同じになってしまいます。イメージとしては「線をつなげていく」です。普通の積分だと、

${\displaystyle \int_{a}^{b} f(x) dx }$

こんな数式です。関数 $f(x)$ を微小区間 $dx$ ごとに分割し、それを $a$ から $b$ までの間で足し合わせていくための計算です。で、微小区間 $dx$ というのは $x$ 軸方向に対しての区間なので、図にしてみるとこうですね。

f:id:takunology:20200527132821p:plain

なので普通に積分すれば面積が求められるわけです。

2. 線積分

では線積分はどうなるかというと、こうなります。

${\displaystyle \int_{C} f(x, y) ds }$

さっきと変わった点は関数が2変数関数になったことと、 $dx$ から $ds$ になったことです。あと積分区間が $C$ になっています。けど、これだけではさっぱりですね。

2.1 直線の長さ

こんな図を用意しました。左側は3次元空間、右側は2次元空間です。

f:id:takunology:20200527140225p:plain

先に右側の赤い線の長さ $l$ を求めてみます。2次元のベクトルと考えれば三平方の定理を使って

${\displaystyle l = \sqrt{x^{2} + y^{2}} }$

で求められます。同様にして左側の緑色の線は3次元のベクトルと考えて、

${\displaystyle l = \sqrt{x^{2} + y^{2} + z^{2}} }$

で求められます。

2.2 曲線の長さ

ただ、曲線はそう簡単には求まりません。位置によって "くねくね" しているので変化量が一定ではありません。

しかし、どんな曲線でも微小な区間ごとに取り出してみると直線とみなせます。まずは上からみた図として2次元空間に落としてきます。

f:id:takunology:20200527142355p:plain

これで関数を線としてみなすことができます。ここからさらに線を直線で表していきます。直線にするには微小区間に分けてつなげていけばいいので、

f:id:takunology:20200527143854p:plain

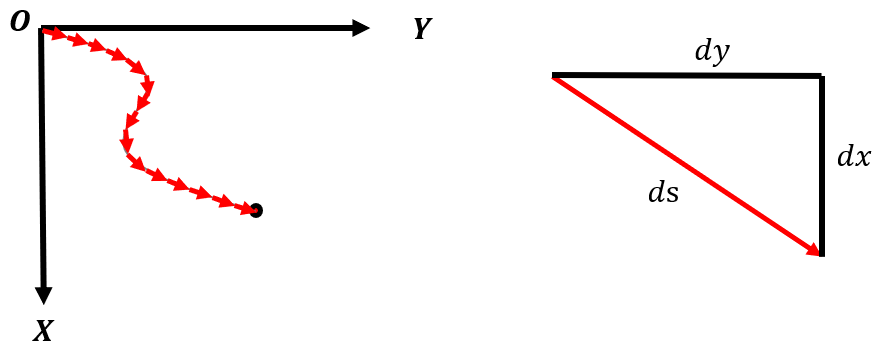
こうなります。矢印1つあたりの変化（傾き）は $ds$ になります。で、この $ds$ は直線の式に当てはめることができます。

${\displaystyle ds = \sqrt{dx^{2} + dy^{2}} }$

これを連続してつないでいくことによって曲線を実現できるのですが、変化は位置によって異なります。ただ、位置は $dx, dy$ に依存しているので1変数だけを動かすわけにはいきません。なので、2変数を一気に変化させることのできるように工夫します。

2.3 時間を取り入れる

位置を変えるために時間を取り入れて、瞬間的な時間変化を $dt$ とします。すると、微小区間の直線の長さ $ds$ は成分 $dx, dy$ によって決まります。さらに、これら成分は時間によって変化するのでそれぞれ $dx(t), dy(t)$ となります。

「時間によって変化する」→ 「時間で微分できる」→ 「刻々の変化（直線の長さ）が求められる」という流れです。

${\displaystyle \frac{ ds(dx(t), dy(t)) }{dt} = \sqrt{ \left( \frac{dx(t)}{dt} \right)^{2} + \left( \frac{dy(t)}{dt} \right)^{2} } }$

あとは時々刻々の直線の長さを足し合わせていけばいいので、微小区間の直線の長さ $ds$ を連続してつなげばいいことになります。なので、上の式を線積分の式に代入してみると、微小時間 $dt$ で積分すれば

${\displaystyle \int_{C} f(x(t), y(t)) \sqrt{ \left( \frac{dx(t)}{dt} \right)^{2} + \left( \frac{dy(t)}{dt} \right)^{2} } \ dt }$

となります。ただし、関数 $f(x, y)$ は時間変化を考慮して $f(x(t), y(t))$ になります。

あとは積分範囲ですが、 $dt$ なので時間の積分（あるいは経路による積分）です。ただ、 $C$ となっているのは、この積分が「線積分である」という意味を示しており、これ以上の意味は特にないです。おそらくですが、曲線を英語にしたときに "Curve" となることから $C$ と書いているのかもしれません。

あと、3次元における線積分はこうなります。成分を拡張しただけです。

${\displaystyle \int_{C} f(x(t), y(t), z(t)) \sqrt{ \left( \frac{dx(t)}{dt} \right)^{2} + \left( \frac{dy(t)}{dt} \right)^{2} + \left( \frac{dz(t)}{dt} \right)^{2}} \ dt }$