ヤフーでこんな記事を見つけました。
(リンク先が切れたときのために)
若者が宝くじを買ってくれないそうです。
サイコロの場合
例えばサイコロを振って「4」の目が出た場合、次に出る目は?と聞かれても確率は なので、当たったとしても偶然です。確率が偏っていれば予測できるかもしれませんが、同様に確からしい場合は確率は均等で、次の数字を確実に当てるのは不可能です。仮に偏っている場合は「偏る原因」があるので、それを分析する価値はあります。
宝くじの当せん金率
宝くじも同様です。宝くじで一番当てやすいと言われる「ナンバーズ3」 を例に考えてみます。ナンバーズ3 は 0 ~ 9 までの数字を3桁選び、その組み合わせ(あるいは順番通り)に抽選されれば、見事当選となります。で、その中でも「ミニ」という買い方があり、2桁の数字の順番通りに抽選されれば当選というのもあります。この場合、組み合わせは 10通りを2桁なので、100通りになります。その中で当選すればいいので です。確率は 1% です。かなり厳しい当選確率ですが、現状最も当たりやすい買い方です。
「でも、全部買えばいくらか戻ってくるじゃん?」という人のために計算してみました。(2020年7月10日以前の過去31回のナンバーズ3ミニの当選金額をもとに、計算しています。)
- 平均当選金額 : 9173円
- 中央値 : 8900円
- 標準偏差 : 2025円
- 当せん金率 : 45.9 %
ちなみにナンバーズ3は1口200円で販売されているので、当たれば平均 9173 円戻ってきます。みずほ銀行が公開している理論値は 9000円 なので、まぁ妥当と言えば妥当です。中央値もそんな感じですね。ソース貼っておきます。
中央値を算出した理由は、最高当選金額が 12800円 で最低当選金額が 3300 円だったためです。だいぶ偏りがありました。
全て買うと1口200円 100通りなので2万円です。平均当選金額で割ると、だいたい 45.9% 戻ってくる計算になります。標準偏差は平均当選金額から離れた値です。だいたい 2025円前後で収まるようです。当選金率は総務省の資料がありました。ほぼ一致しています。
https://www.soumu.go.jp/main_content/000084191.pdf
ちなみに、標準化した(平均 = 0, 標準偏差 = 1)場合はこんな感じです。

過去31回分なのでなんとも言えませんが、マイナスに偏りがある(平均より小さい)のが気になるところですね。
頻出数字の話
「頻出数字に絞って当てればいいじゃん」という人のために計算してみました。(2020年7月10日まで5475回分のデータ)
こちらが当選数字です。
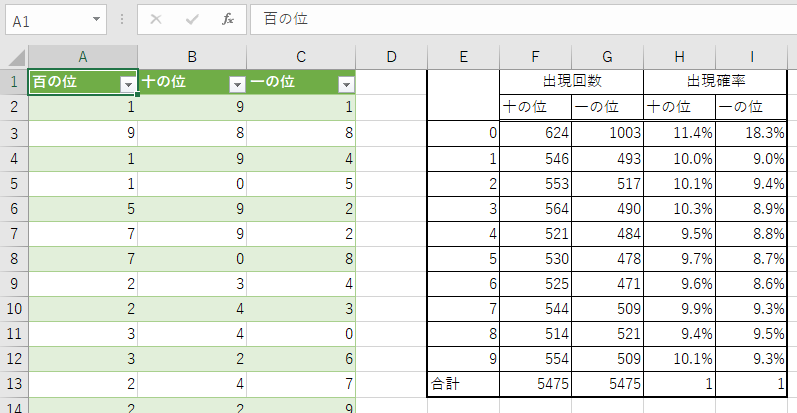
こちらが乱数関数(RANDBETWEEN)を用いて5476回数分繰り返した場合です。
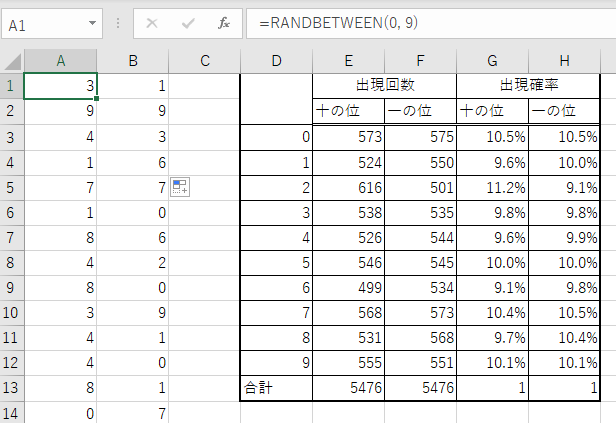
どうですかね?0が出やすいようですが...。0が出やすいといっても 18% の確率で出るので微妙ですね。(せめて50%なら2択に絞れるのですが...)
Excelで乱数をぶん回しても同じような確率になるので、予測はかなり厳しいと思います。
結論
私としての結論は「買い続けるほど損する」です。「宝くじは夢を買う」なんて言いますがその通りだと思います。嗜む程度ならいいかなと思いますが、進んで買おうとは思えませんでした。当せん金率が半分もいかないのはちょっと...ね...。
宝くじのからくりを知ってしまうと、買わない傾向にあるのも納得です。
参考文献
統計学入門
統計学の図鑑

